こんにちは。 山師です。
夏休みももうすぐ終わりですね。 私は実験と論文執筆をして夏休みを過ごしました。 今回は物理が関係した数値計算の記事を書きます。 具体的には、水素様原子の電子の非束縛状態を計算する話です。
ディラック方程式と非束縛状態
重い1つの電荷 (原子核) が中心にあり、軽い1つの電荷 (電子) がそのまわりを運動するような系を考えます。 そのような系を表す相対論的方程式の解は厳密に求められており、大きく分けて2種類の解があります。 ひとつは束縛状態で、もうひとつは非束縛状態です。 束縛状態では電子は原子核のまわりを運動しつづけますが、非束縛状態ではどこまでも遠くへ行ってしまいます (原子核からの距離の期待値が発散する) 。
ディラック方程式
ディラック方程式 (Dirac equation) は、電子などのスピン1/2の粒子の運動を表す相対論的な方程式です。 $$\left( \vec{\alpha} \cdot \vec{p} + \beta m_e + V(x) \right) \psi (x) = E \psi (x)$$ ここで、\(\alpha\)および\(\beta\)はディラック行列として知られる\(4 \times 4\)の行列です。 波動関数 \(\psi(x)\) は4成分を持ちます。
変数分離
非束縛電子の (ディラック方程式の意味での) 波動関数は、次のように2成分ごとに変数分離できます。$$\psi = \frac{1}{r} \begin{pmatrix} P_{E \kappa} (r) \chi_{\kappa m} (\theta, \phi) \\ i Q_{E\kappa} (r) \chi_{-\kappa m} (\theta, \phi) \end{pmatrix}$$ ここで、\(P\)および\(Q\)はスカラー関数、\(\chi\)は2成分の角度方向の関数です[1]球面調和関数のお化けみたいなやつ。 相対論的量子力学の本とかに定義が書いてあるはず。。
\(P\)および\(Q\)は、クーロンポテンシャル\(V(r) = -e^2/r\)に対しては解析解が求められており、次のようになります[2]J. Eichler and T. Stöhlker. Physics Reports 439, 1-99 (2007).。 \begin{align} P_{E\kappa} &= \mathfrak{N} (E+m)^{1/2} r (2pr)^{s-1} {\rm Re} \left[ e^{-ipr} e^{i\delta_\kappa} (s+i\eta) M_{2s+1}^{s+1+i\eta} (2ipr) \right] \\ Q_{E\kappa} &= – \mathfrak{N} (E-m)^{1/2} r (2pr)^{s-1} {\rm Im} \left[ e^{-ipr} e^{i\delta_\kappa} (s+i\eta) M_{2s+1}^{s+1+i\eta} (2ipr) \right] \end{align} ここで、\(\mathfrak{N}\)は規格化定数で、\begin{align} \eta &= \alpha Z E / p \\ s &= \sqrt{\kappa^2 – \alpha^2 Z^2} \\ \delta_\kappa &= \frac{1}{2} {\rm arg} \left( \frac{-\kappa+i\eta/E}{s+i\eta} \right) \end{align} です。 \(Z\)は原子番号で、\(\alpha\)は微細構造定数 (fine-structure constant) です。 \(M\)は次のような多項式です。\begin{align} M_b^{a} (\rho) &= 1 + \frac{(a)_0}{(b)_0} \frac{\rho}{1!} + \frac{(a)_1}{(b)_1} \frac{\rho^2}{2!} + … + \frac{(a)_n}{(b)_n} \frac{\rho^n}{n!} + … \\ (a)_n &= a (a+1) (a+2) … (a+n-1) \end{align} なんだかとても複雑ですね。
描画してみよう
実際に、上に示した解析解をプロットしてみましょう。 コードは以下のようになります。 エネルギーはリュードベリ定数 (Rydberg constant) 単位で、長さはボーア半径 (Bohr radius) で与えています。 規格化は適当です。
import math, cmath
import numpy as np
import matplotlib.pyplot as plt
from scipy import special
import mpmath
mpmath.dps = 25
mpmath.pretty = True
ALPHA = 1.0 / 137.036
RYDBERG_keV = 13.605693e-3
BOHR_m = 5.2917721e-11
MC2 = 510.998950 / RYDBERG_keV
Z = 14
KAPPA = -1
p = 0.1 * MC2
R_MIN = 1.0e-3
R_MAX = 5.0
E = math.sqrt(MC2**2 + p**2)
SIGMA = math.sqrt(KAPPA**2 - (ALPHA**2)*(Z**2))
ETA = ALPHA * Z * E / p
DELTA = 0.5 * cmath.phase((-KAPPA+1.0j*ETA*MC2/E) / (SIGMA+1.0j*ETA))
NORM = math.sqrt(2.0*(p/MC2) / math.pi) * math.exp(0.5*math.pi*ETA) * abs(special.gamma(SIGMA+1.0j*ETA)) / special.gamma(2.0*SIGMA+1.0)
def M_mp(a, b, r) :
m = mpmath.hyp1f1(a, b, r)
return m
def P(r) :
pr = p*r*ALPHA/2.0
t1 = math.pow(2.0*pr, SIGMA-1.0)
t2 = cmath.exp(-1.0j*pr) * cmath.exp(1.0j*DELTA) * (SIGMA+1.0j*ETA) * M_mp(SIGMA+1.0+1.0j*ETA, 2.0*SIGMA+1.0, 2.0j*pr)
t3 = r*MC2*ALPHA/(4.0*math.pi)
val = NORM * math.sqrt(E/MC2 + 1.0) * t1 * t2.real * t3
return val
def Q(r) :
pr = p*r*ALPHA/2.0
t1 = math.pow(2.0*pr, SIGMA-1.0)
t2 = cmath.exp(-1.0j*pr) * cmath.exp(1.0j*DELTA) * (SIGMA+1.0j*ETA) * M_mp(SIGMA+1.0+1.0j*ETA, 2.0*SIGMA+1.0, 2.0j*pr)
t3 = r*MC2*ALPHA/(4.0*math.pi)
val = - NORM * math.sqrt(E/MC2 - 1.0) * t1 * t2.imag * t3
return val
a_r = np.arange(R_MIN, R_MAX, 1.0e-3);
a_P = [P(r) for r in a_r]
a_Q = [Q(r) for r in a_r]
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax1.plot(a_r, a_P, label = "P")
ax1.set_xlabel("r (Bohr radius)")
ax1.set_xlim(0.0, R_MAX)
ax1.legend(loc = "lower right")
ax2 = fig.add_subplot(2, 1, 2)
ax2.plot(a_r, a_Q, label = "Q")
ax2.set_xlabel("r (Bohr radius)")
ax2.set_xlim(0.0, R_MAX)
ax2.legend(loc = "lower right")
plt.show()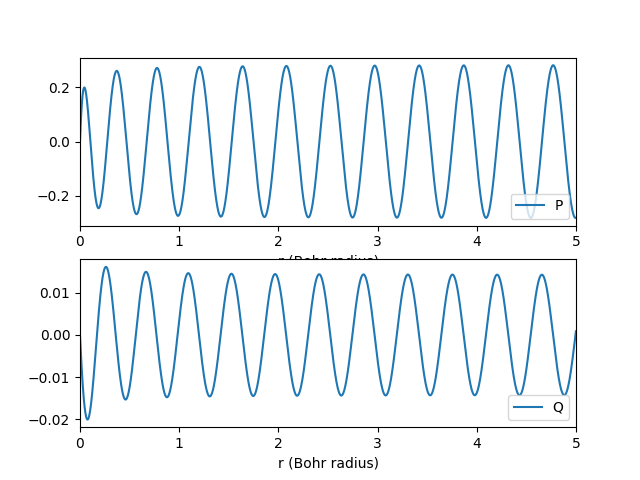
数値計算
以上のように解析解があるわけですが、これには問題もあります。 もっとも大きな問題が、クーロンポテンシャル以外には適用できない点です。 実際の原子では、電子間反発だったり、原子核の大きさだったり、色々な効果が入ってきます。
微分方程式を解く
そこで、今度は微分方程式を解くやり方で数値計算してみましょう。 この方法では、ポテンシャルはクーロンポテンシャルに限られません。 以下に示す方法はZhang, Sampson, and Mohanty[3]H. L. Zhang, D. H. Sampson, and A. K. Mohanty. Physical Review A 40, 616 (1989).によります。 なお、以降はZSM論文に合わせて長さの単位をボーア半径 (Bohr radius) 、エネルギーの単位をリュードベリ定数 (Rydberg constant) とします。
まず、\(P\)に関して次のような置き換えをします。 $$F_{E\kappa}(r) = \frac{P_{E\kappa}(r)}{\sqrt{a_P(r)}}$$ ここで、$$a_P(r) = \frac{\alpha}{2} \left( E – V(r) + \frac{4}{\alpha^2} \right)$$ です。 \(F_{E\kappa}(r)\) の満たすべき微分方程式は次のようになります。 $$\frac{{\rm d}}{{\rm d}r} F_{E\kappa}(r) + \omega(r) F_{E\kappa}(r) = 0$$ ここで、\begin{align}\omega(r) =& a_P(r) a_Q(r) – \frac{l(l+1)}{r^2} – \frac{\kappa}{r}\frac{1}{a_P(r)}\frac{{\rm d}}{{\rm d}r}a_P(r) \\ & \quad – \frac{3}{4} \left( \frac{1}{a_P(r)}\frac{{\rm d}}{{\rm d}r}a_P(r) \right)^2 + \frac{1}{2} \frac{1}{a_P(r)}\frac{{\rm d}^2}{{\rm d}r^2}a_P(r)\end{align} また、 $$a_Q(r) = \frac{\alpha}{2} \left( E – V(r) \right)$$ です。 この方程式を数値計算で解けばよいというわけです。 これもまた複雑ですね。 \(Q_{E\kappa}\) を求める際には、$$\left( \frac{{\rm d}}{{\rm d}r} + \frac{\kappa}{r} \right) P_{E\kappa} (r) = a_P(r) Q_{E\kappa} (r)$$ で計算できます。
計算してみよう
実際に微分方程式を解いた結果をプロットしてみましょう。 安定した結果を得るために、陰解法であるCrank-Nicolson法[4]Wikipediaの記事を参照。 ちなみに、4次のルンゲクッタ法を用いると発散しました。を用いています。
import math
import numpy as np
import matplotlib.pyplot as plt
ALPHA = 1.0 / 137.036
HC = ALPHA / (4.0*math.pi)
RYDBERG_keV = 13.605693e-3
BOHR_m = 5.2917721e-11
MC2 = 510.998950 / RYDBERG_keV
Z = 14
KAPPA = -1
p = 0.1 * MC2
R_MIN = 1.0e-3
R_MAX = 5.0
E = math.sqrt(MC2**2 + p**2) - MC2
l = KAPPA
if KAPPA < 0 :
l = -KAPPA-1
def V(r) :
return - 2.0*Z / r
def a_P(r) :
return 0.5*ALPHA * (E - V(r) + 4.0/(ALPHA**2))
def a_Q(r) :
return 0.5*ALPHA * (E - V(r))
def omega(r, eps = 1.0e-8) :
dr1a = (a_P(r+eps) - a_P(r-eps)) / (2.0*eps)
dr2a = (a_P(r+eps) - 2.0*a_P(r) + a_P(r-eps)) / (eps**2)
t1 = a_P(r) * a_Q(r)
t2 = l*(l+1) / (r**2)
t3 = (KAPPA/r) * (1.0/a_P(r)) * dr1a
t4 = 0.75 * ((dr1a / a_P(r))**2)
t5 = 0.5 * dr2a / a_P(r)
return t1-t2-t3-t4+t5
def do_calc(r_min, r_max, r_step = 1.0e-3) :
a_r = np.arange(r_min, r_max, r_step)
a_f = np.zeros((len(a_r), 2))
a_p = np.zeros((len(a_r), ))
a_q = np.zeros((len(a_r), ))
if KAPPA == -1 :
a_f[0, 0] = 1.0
for i in range(len(a_r)-1) :
r = a_r[i]
# derive F
det = 1.0 + 0.25*(r_step**2)*omega(r+r_step)
a_f[i+1, 0] = ((1.0-0.25*(r_step**2)*omega(r+r_step))*a_f[i, 0] + (-0.5*r_step*(omega(r)+omega(r+r_step)))*a_f[i, 1]) / det
a_f[i+1, 1] = (r_step*a_f[i, 0] + (1.0-0.25*(r_step**2)*omega(r))*a_f[i, 1]) / det
# derive P and Q
a_p[i+1] = math.sqrt(a_P(r+r_step))*a_f[i+1, 1]
a_q[i+1] = ((a_p[i+1]-a_p[i])/r_step + (KAPPA/(r+r_step))*a_p[i+1]) / a_P(r)
return a_r, a_p, a_q
a_r, a_p, a_q = do_calc(R_MIN, R_MAX)
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax1.plot(a_r, a_p, label = "P")
ax1.set_xlabel("r (Bohr radius)")
ax1.set_xlim(0.0, R_MAX)
ax1.legend(loc = "lower right")
ax2 = fig.add_subplot(2, 1, 2)
ax2.plot(a_r, a_q, label = "Q")
ax2.set_xlabel("r (Bohr radius)")
ax2.set_xlim(0.0, R_MAX)
ax2.legend(loc = "lower right")
plt.show()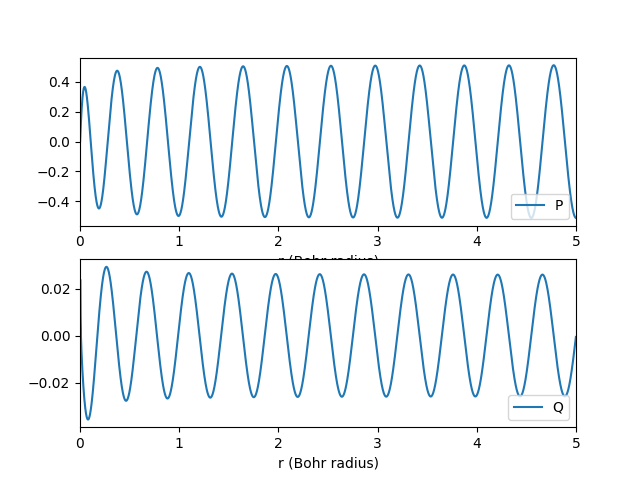
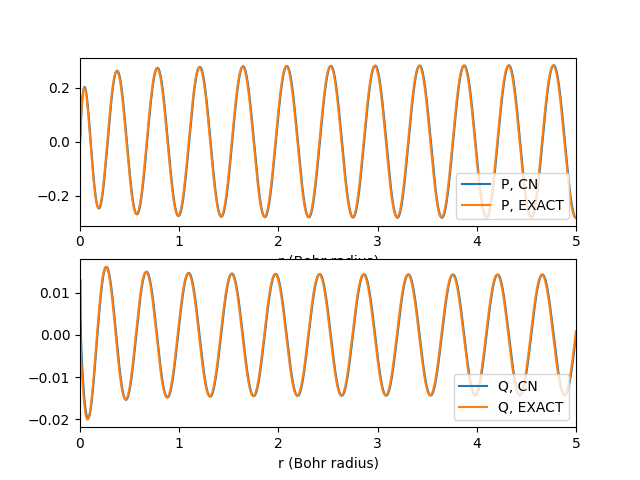
まとめ
この記事では、水素様原子の電子の非束縛状態を計算する方法について書きました。 完全に私の趣味みたいな記事になりましたが、数値計算の方法自体は他の問題にも応用できると思って公開します。
脚注
| ↑1 | 球面調和関数のお化けみたいなやつ。 相対論的量子力学の本とかに定義が書いてあるはず。 |
|---|---|
| ↑2 | J. Eichler and T. Stöhlker. Physics Reports 439, 1-99 (2007). |
| ↑3 | H. L. Zhang, D. H. Sampson, and A. K. Mohanty. Physical Review A 40, 616 (1989). |
| ↑4 | Wikipediaの記事を参照。 ちなみに、4次のルンゲクッタ法を用いると発散しました。 |