こんにちは。 山師です。
今回は少し計算機寄りのことを書こうと思います。 具体的には、反応断面積を \(\theta\) 方向の極座標にプロットする方法についてです。
何をしたいか
目的
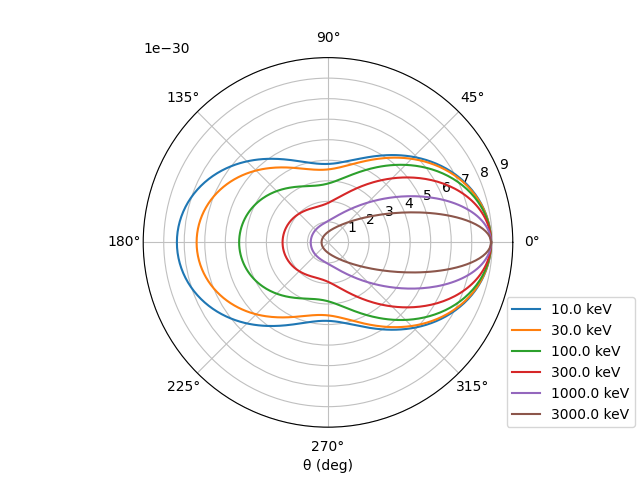
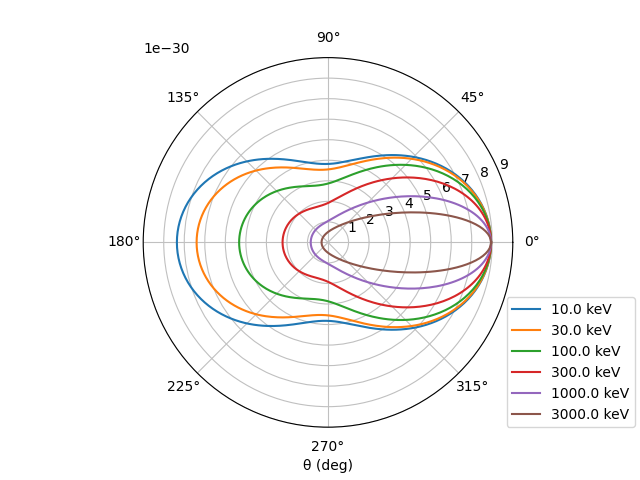
修士論文を書くとき、電子の反応断面積の図を作る必要がありました。 具体的には、コンプトン散乱の微分散乱断面積の図を作って、レビューパートに載せました。 どうせ載せるなら綺麗な図で、しかも先輩からのお下がりではない図を載せたいと思ったので、自分でコードを書くことにしました。
物理学的背景
場の量子論によれば、無偏光に対する静止した自由電子のコンプトン散乱断面積は、次に示される Klein-Nishina の公式で与えられます。 $$\frac{d\sigma}{d\Omega} = \frac{1}{2} {r_0}^2 \left( \frac{E}{E_0} \right)^2 \left( \frac{E}{E_0} + \frac{E_0}{E} – \sin^2 \theta \right)$$ ここで、\(r_0\) は電子の古典半径、 \(E_0\) および \(E\) はそれぞれ散乱前後の光子のエネルギーです。 \(\theta\) は光子の入射方向に対する散乱方向を表します。 \(E_0\) と \(E\) との間には次の関係があります。 $$E_0 – E = \frac{E_0}{m_e c^2} \left( 1 – \cos \theta \right)$$ ここで、\(m_e = 511 {\rm\ keV} / c^2\) は電子の静止質量です。
コード
以下に Python でのコードを示します。 numpy と matplotlib を使用しています。
import math
import numpy as np
import matplotlib.pyplot as plt
# energy of incoming photons
E_INIT = [10.0, 30.0, 100.0, 300.0, 1000.0, 3000.0] # keV
def energy_ratio(e_init, theta) :
return 1.0 / (1.0 + (e_init / 511.0) * (1 - math.cos(theta)))
# r0 [m]
def KN_cross_diff(e_init, theta, r0 = 2.818e-15) :
hoge = energy_ratio(e_init, theta)
s = math.sin(theta)
return 0.5 * r0 * r0 * hoge * hoge * (hoge + 1.0 / hoge - s * s)
def plot_KN_cross(e_init) :
for e in e_init :
x = np.linspace(0, 360, 361)
y = np.array([KN_cross_diff(e, math.pi * ang / 180.0) for ang in x])
plt.polar(x * math.pi / 180.0, y, label='%.1f keV'%(e))
plt.grid(b = True, color='silver')
plt.xlabel('\u03B8 (deg)')
plt.ylim([0.0, 9.0e-30])
plt.legend(loc='lower right', borderaxespad=0, ncol=1, bbox_to_anchor=(1.33, 0.0))
plt.show()
def main() :
plot_KN_cross(E_INIT)
# magic code
if __name__ == '__main__' :
main()plt.polar を使うのがミソです。 蟹ミソ食べたい。
結果
python3 plot_KN.py単位は \({\rm m^2 / Sr}\) で出力されます。